測定原理（静的接触角）

主な接触角の測定原理をご紹介します。

図１は、「気体（空気）」中において、固体に液体（液滴）がぬれた平衡状態を、真横から見た様子を表しています。

液滴と固体表面との境界線と、境界点を通る液滴の接線とがなす角度（図１におけるθ）を接触角といいます。液体には表面張力があり、同様に固体にも表面張力があります（特に固体の表面張力のことを、「表面自由エネルギー」と呼ぶことがあります）。この相互作用によって接触角が定まります。

この時、ヤング（Young）の式より、

γ_{SV} = γ_{LV} \cos θ + γ_{SL}

が成り立ちます。

接触角計は、直接接触角θを求めることにより、濡れの相互作用を数値化する装置です。

θ/2法 (A half-angle Method)

θ/2法は、液滴の輪郭が円の一部であるという仮定で、接触角を求める方法です。

接触角の測定に一般的に用いられている測定手法です。

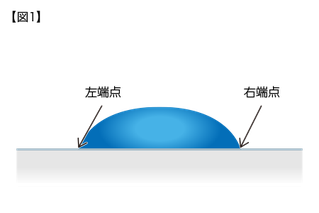
図１にあるように、画像解析により液滴の輪郭座標を抽出し、そこから液滴の左右の端点を求めます。

次に左右の端点を通る直線を境界面とし、左右端転間の垂直二等分線と液滴輪郭の交点を頂点とします（図２）。

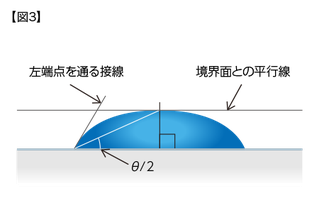
この３点からθ/２を求めることができるため、これにより接触角θを算出することができます。

θ/2法では、液滴の輪郭は円の一部であるという仮定で求めるため、重力の影響を無視できる液滴の量で測定し、左右の接触角は同じ値になります。

液滴の端点近辺を円の一部とみなして、端点での接線を求める接触角測定手法です。

接線法とも呼ばれます。

左右それぞれの接触角を求める事ができますので、左右端点の状態にばらつきが大きくそれぞれの接触角に違いがある場合に有効な測定手法です。

液滴の輪郭を真円の一部とみなして、すべての測定座標を用いて最小二乗法フィッティングを行い、これにより求められた真円の端点における接触角を求める方法です。

Tangent法に比べ、より多くの座標を用いるため、ばらつきが小さくなります。

楕円の方程式は、下記の式で表されます。

\frac{{(x - x_{0})}^{2}}{{R_{x}}^{2}} + \frac{{(y - y_{0})}^{2}}{{R_{y}}^{2}} = 1

ここで $x_{0}$ 、 $y_{0}$ は楕円の中心座標を表します。

$R_{x}$ 、 $R_{y}$ は楕円のX方向半径、Y方向半径です。

特に $R_{x} = R_{y}$ の時、上式は真円を表します。

真円フィッティングまたは楕円フィッティングでは、与えられた輪郭の座標から最小二乗法により、 $x_{0}$ 、 $y_{0}$ 、 $R_{x}$ 、 $R_{y}$ を推定します。

また、上式を任意の点で微分すれば、その点における接線の勾配を求めることができます。すなわち、

\frac{d y}{d x} = \frac{R y^{2} (x - x_{0})}{R x^{2} (y - y_{0})}

左右それぞれの端点の座標と微分後の式から、各端点における接線の勾配を求めることができ、これを使って接触角を求めます。

真円フィッティング法と同様に、液滴の輪郭を楕円の一部とみなして測定する方法です。